data analysis ⊹ data-analysis

Useful R techniques 4: Pretty Heatmap

Kazu Nozue

Tags: RStudio; R; tidyverse

SUMMARY

  • pheatmap() is useful for easy and pretty heatmap
  • Demonstration of example() and demo() function
  • How to reorder columns?
  • How to add annotation bar with custom colors.
example(pheatmap)
## 
## phetmp> # Create test matrix
## phetmp> test = matrix(rnorm(200), 20, 10)
## 
## phetmp> test[1:10, seq(1, 10, 2)] = test[1:10, seq(1, 10, 2)] + 3
## 
## phetmp> test[11:20, seq(2, 10, 2)] = test[11:20, seq(2, 10, 2)] + 2
## 
## phetmp> test[15:20, seq(2, 10, 2)] = test[15:20, seq(2, 10, 2)] + 4
## 
## phetmp> colnames(test) = paste("Test", 1:10, sep = "")
## 
## phetmp> rownames(test) = paste("Gene", 1:20, sep = "")
## 
## phetmp> # Draw heatmaps
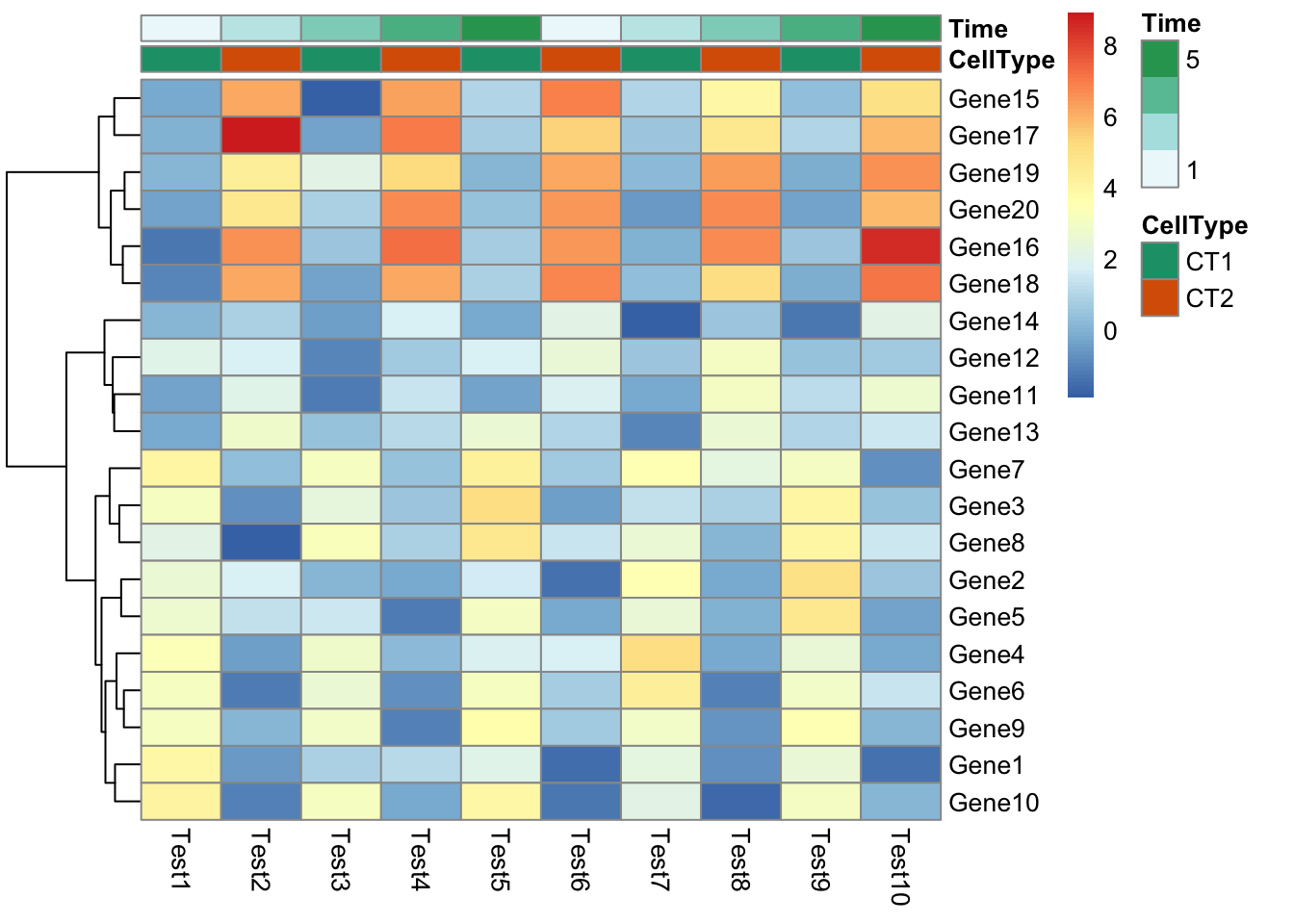
## phetmp> pheatmap(test)

## 
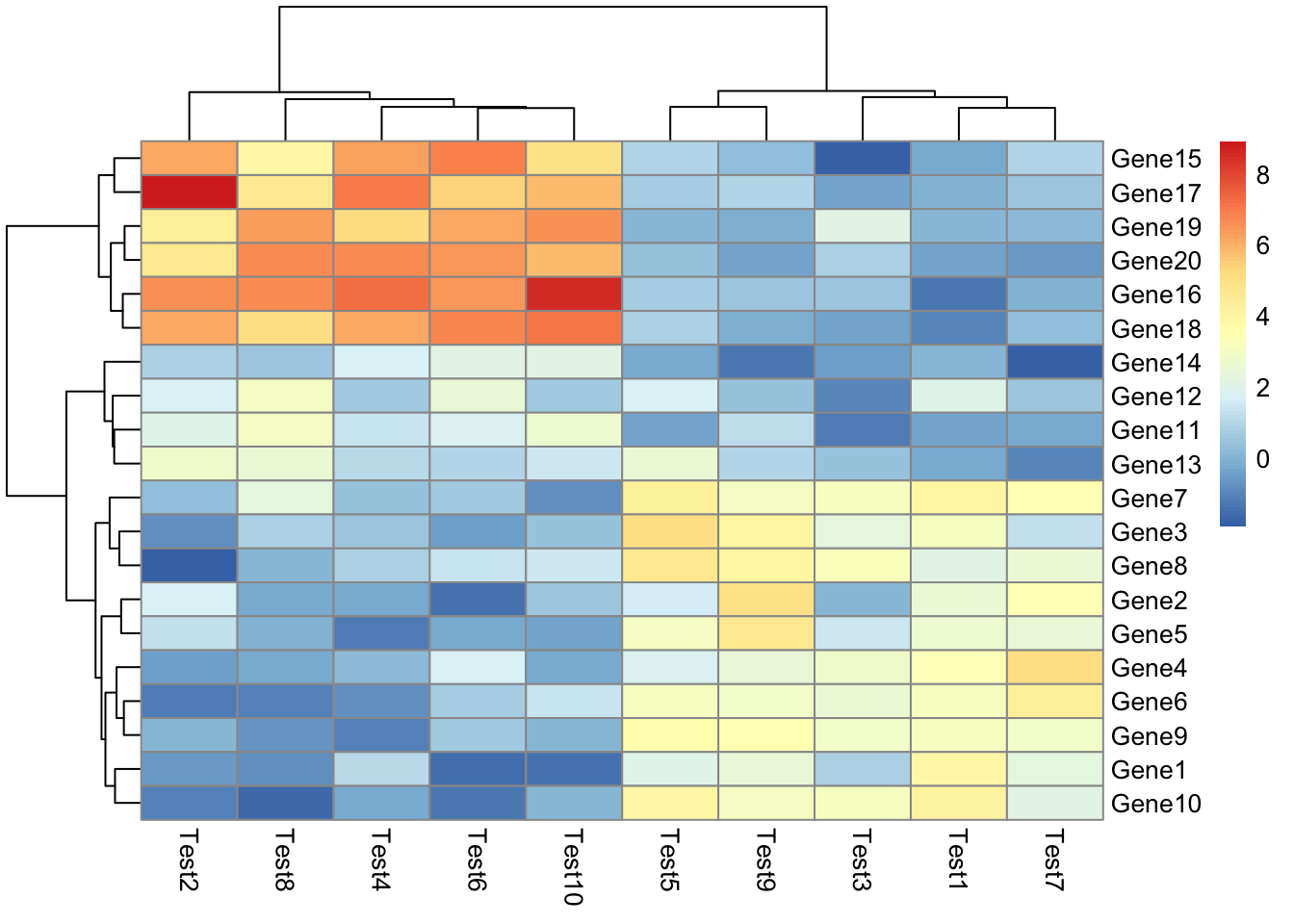
## phetmp> pheatmap(test, kmeans_k = 2)

## 
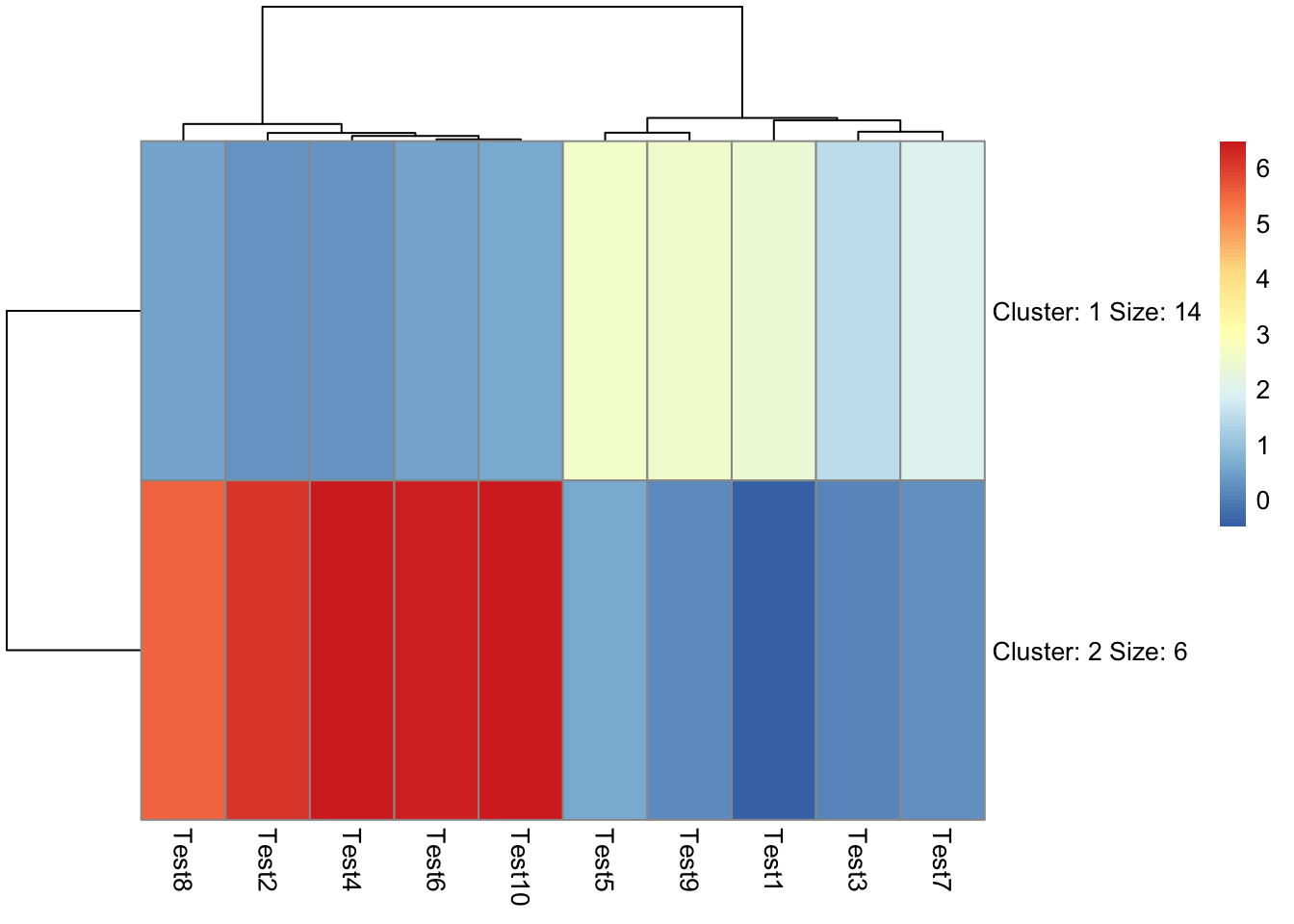
## phetmp> pheatmap(test, scale = "row", clustering_distance_rows = "correlation")

## 
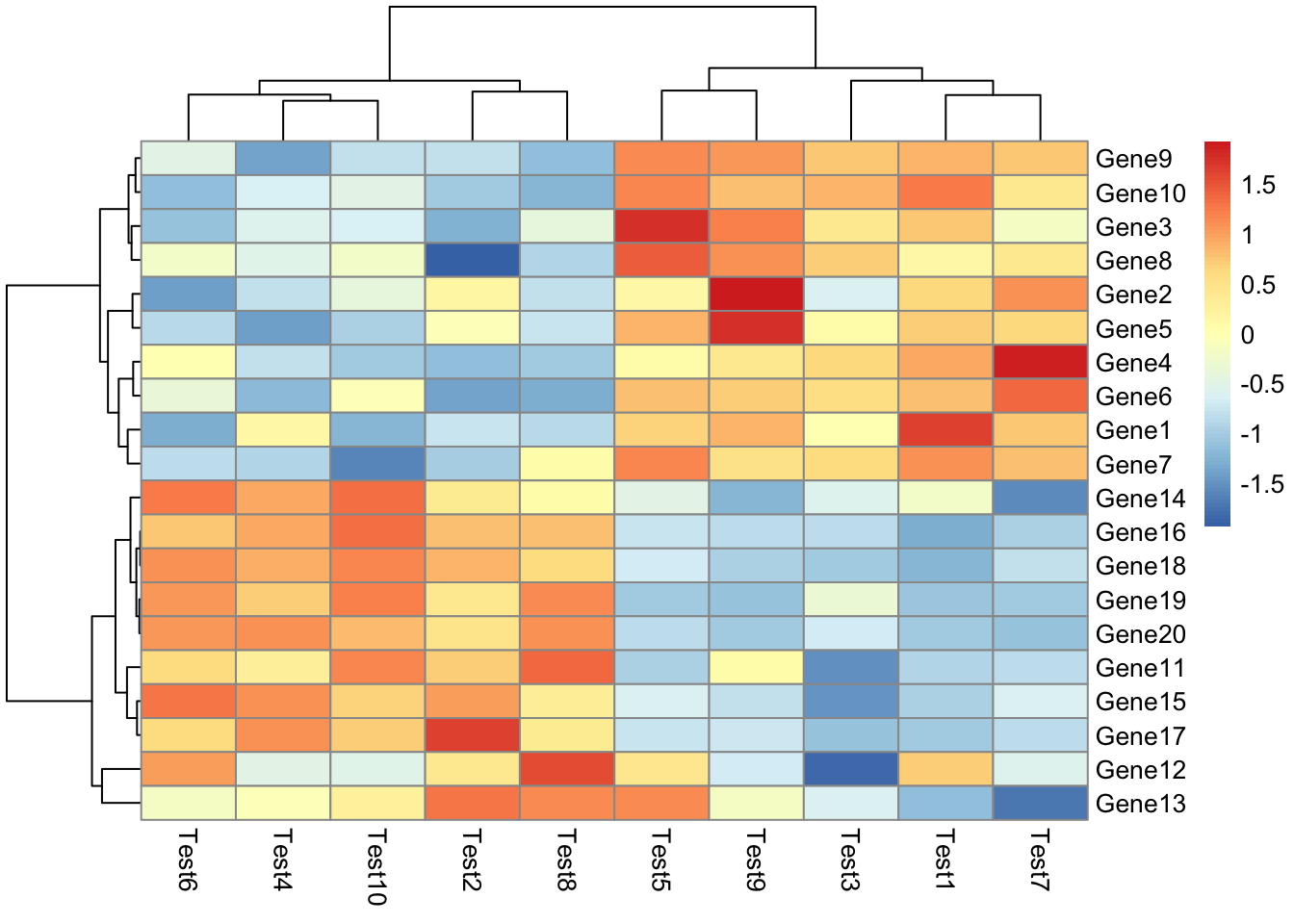
## phetmp> pheatmap(test, color = colorRampPalette(c("navy", "white", "firebrick3"))(50))

## 
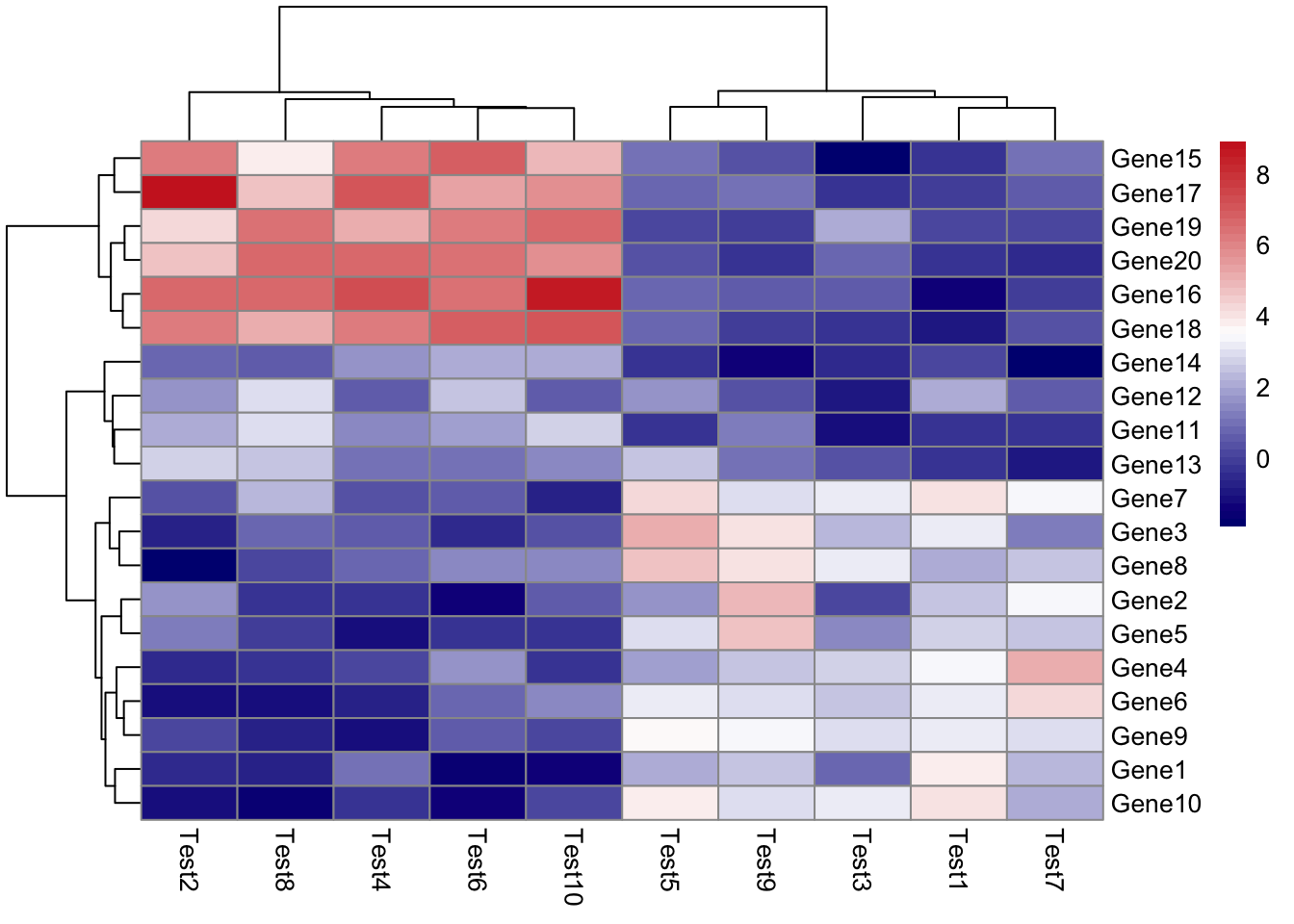
## phetmp> pheatmap(test, cluster_row = FALSE)

## 
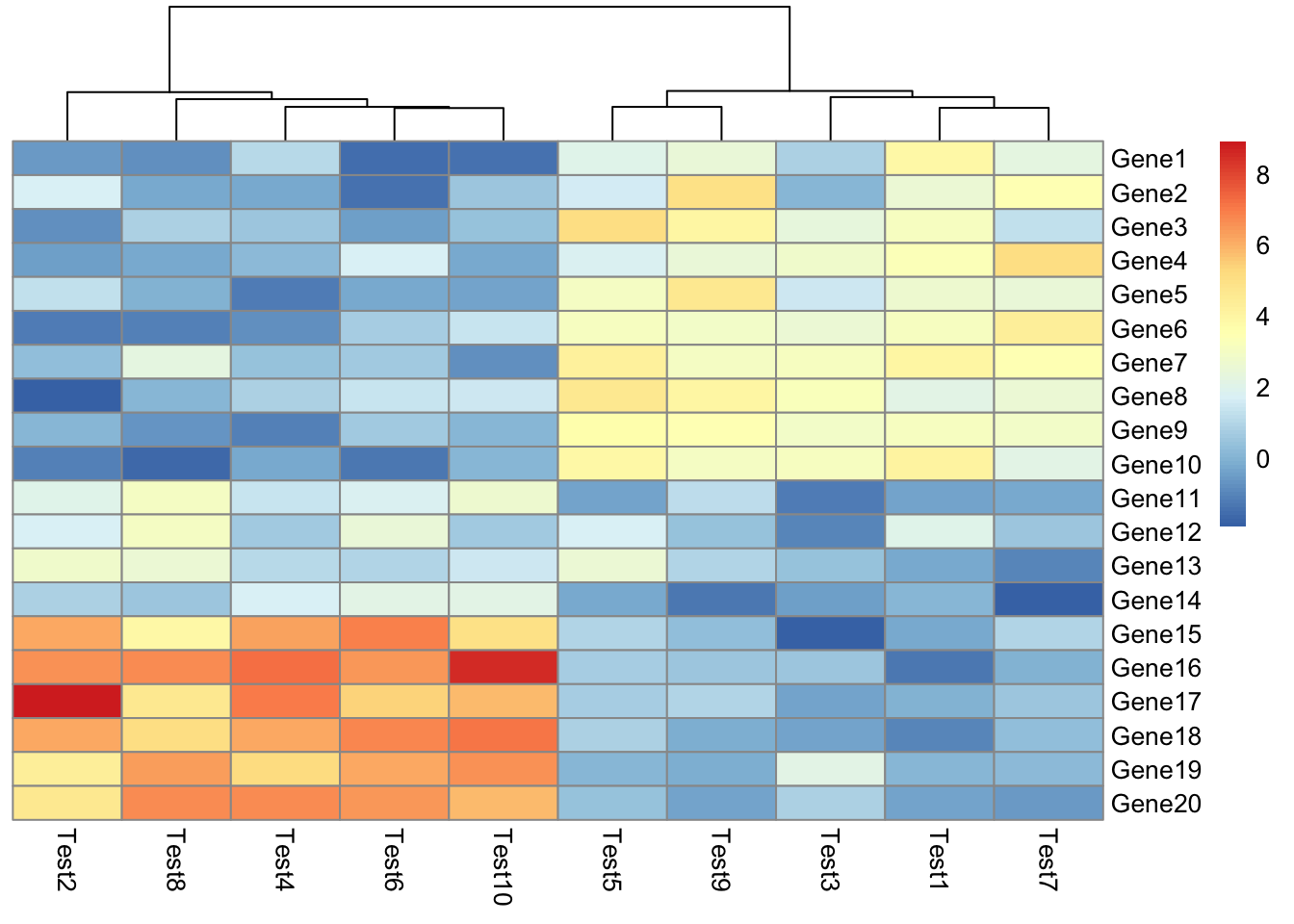
## phetmp> pheatmap(test, legend = FALSE)

## 
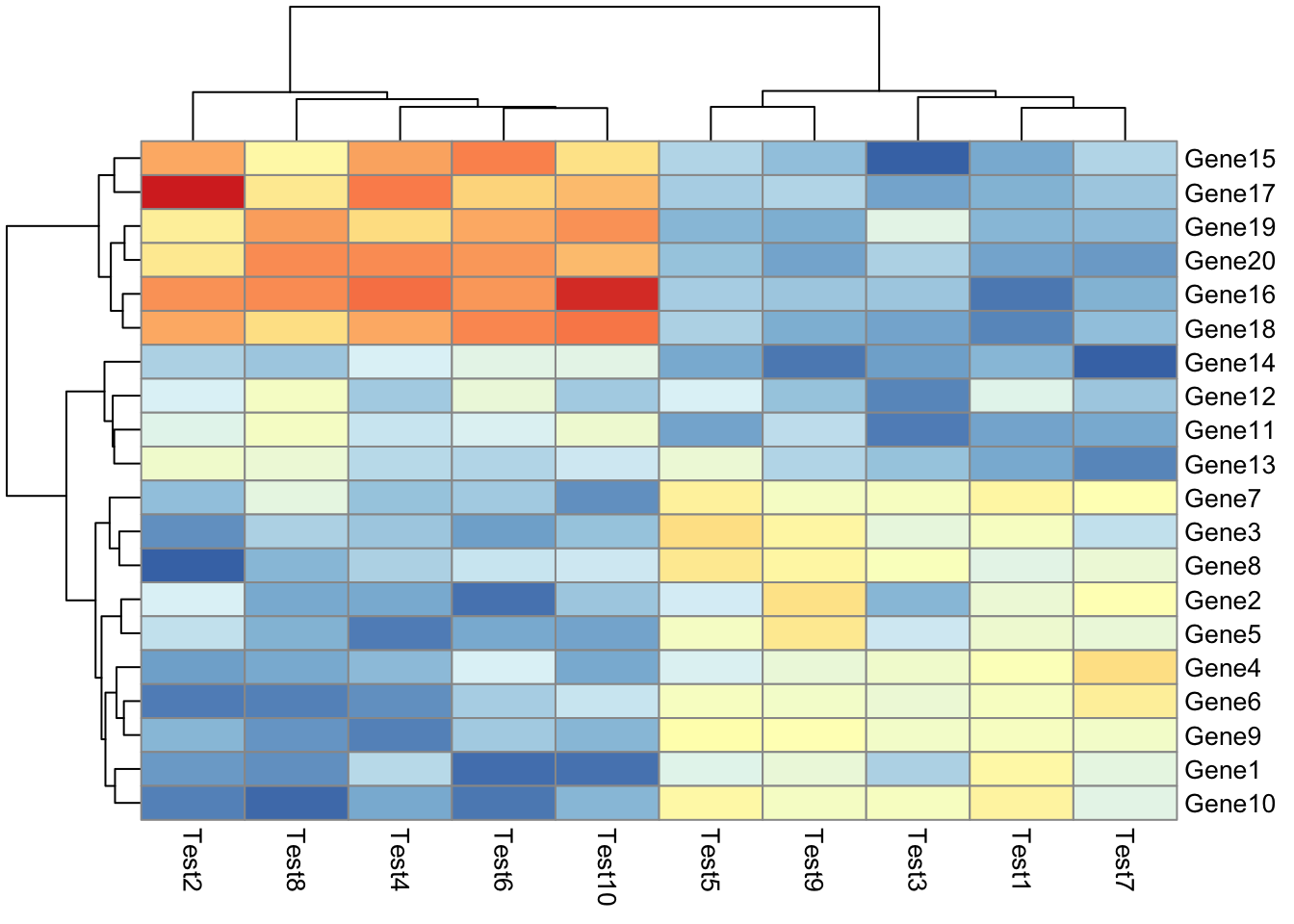
## phetmp> # Show text within cells
## phetmp> pheatmap(test, display_numbers = TRUE)

## 
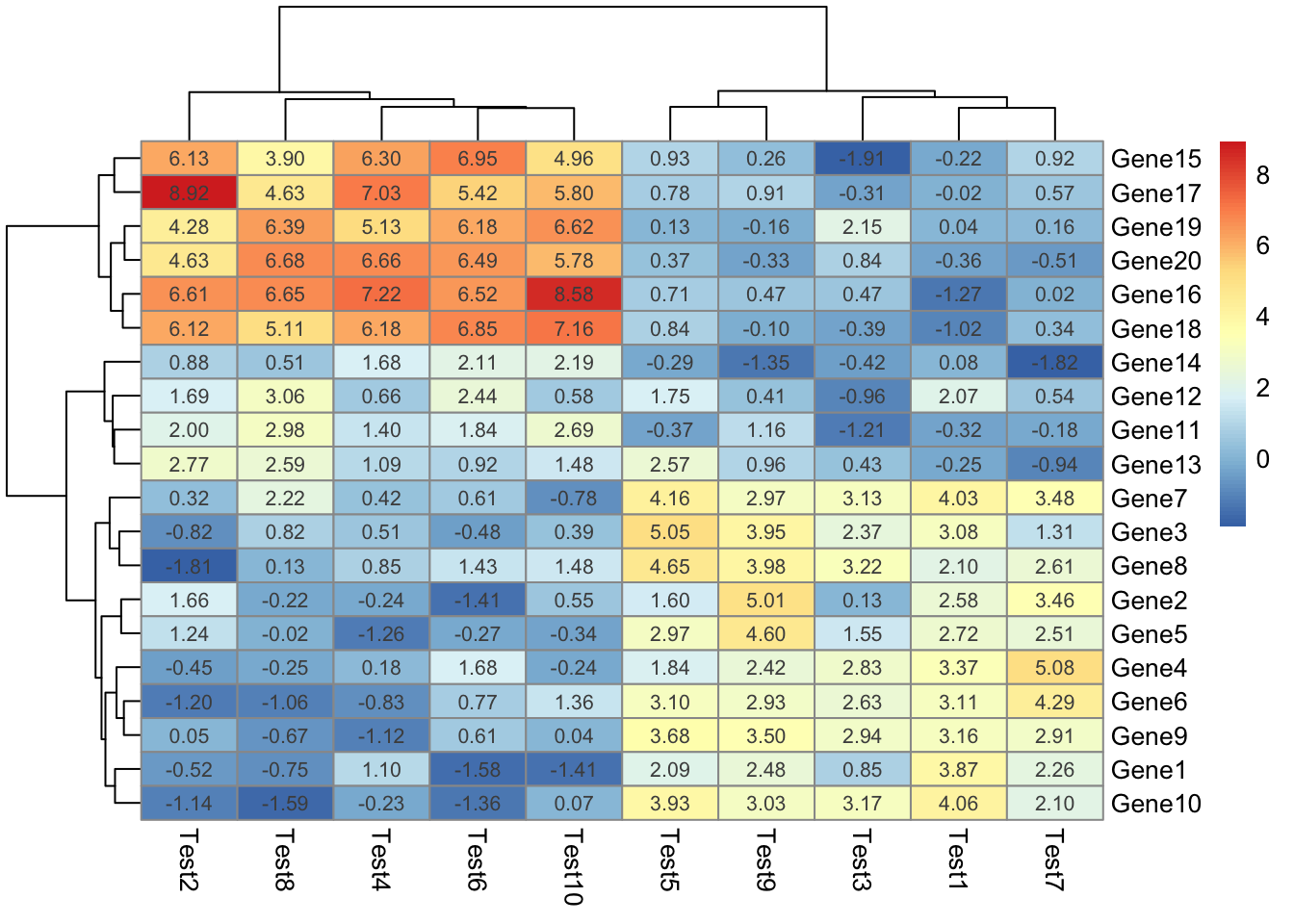
## phetmp> pheatmap(test, display_numbers = TRUE, number_format = "%.1e")

## 
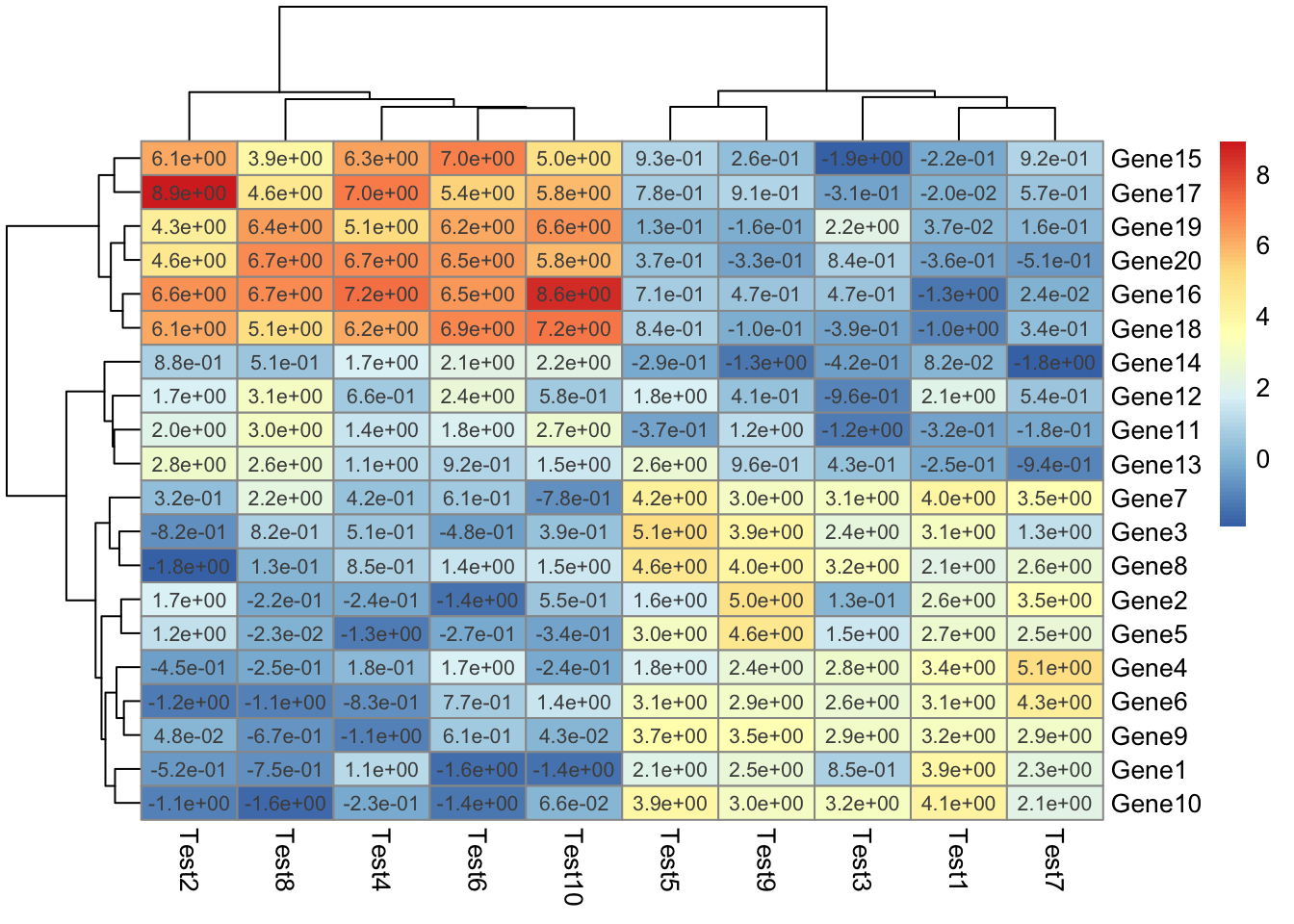
## phetmp> pheatmap(test, display_numbers = matrix(ifelse(test > 5, "*", ""), nrow(test)))

## 
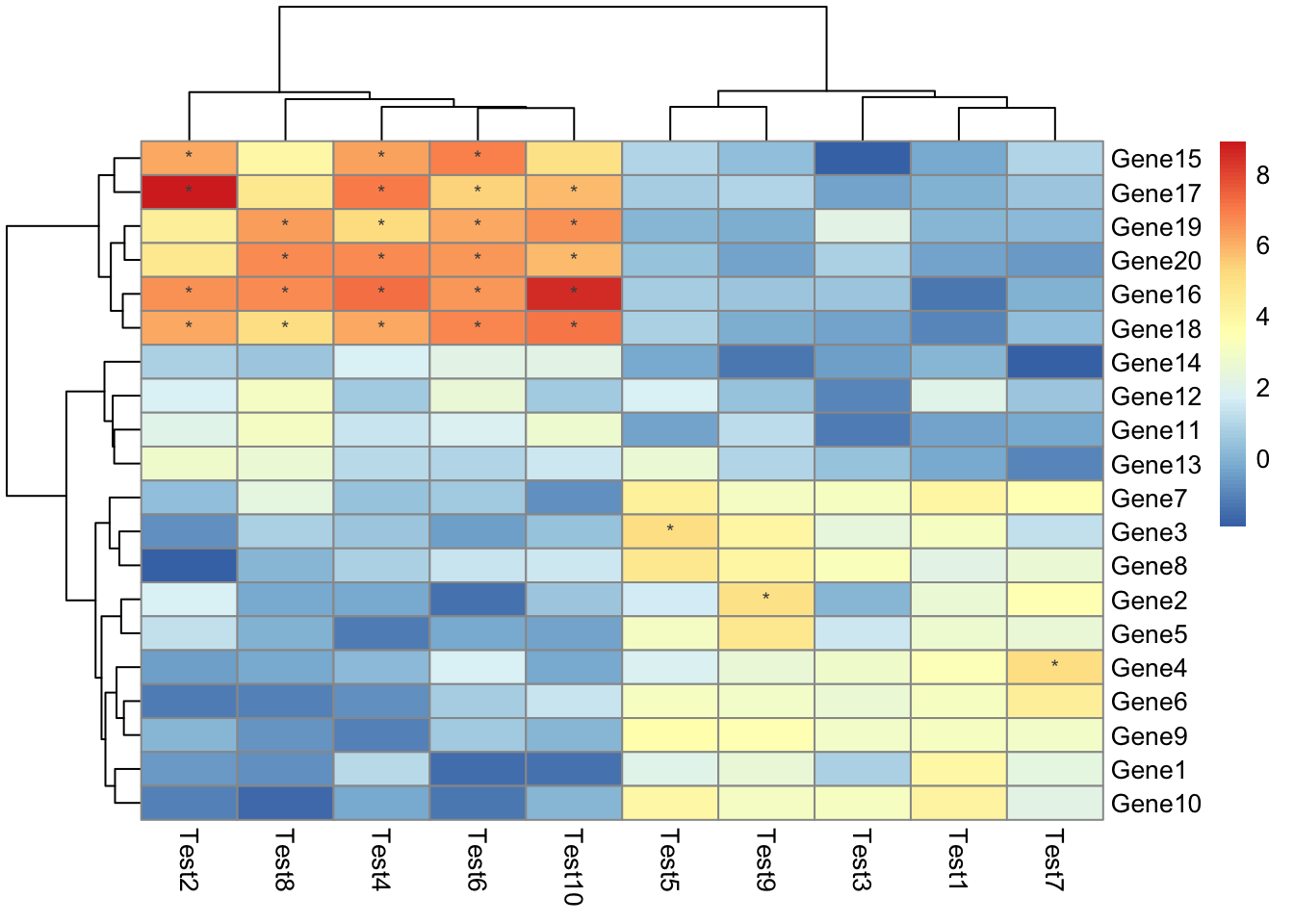
## phetmp> pheatmap(test, cluster_row = FALSE, legend_breaks = -1:4, legend_labels = c("0",
## phetmp+ "1e-4", "1e-3", "1e-2", "1e-1", "1"))

## 
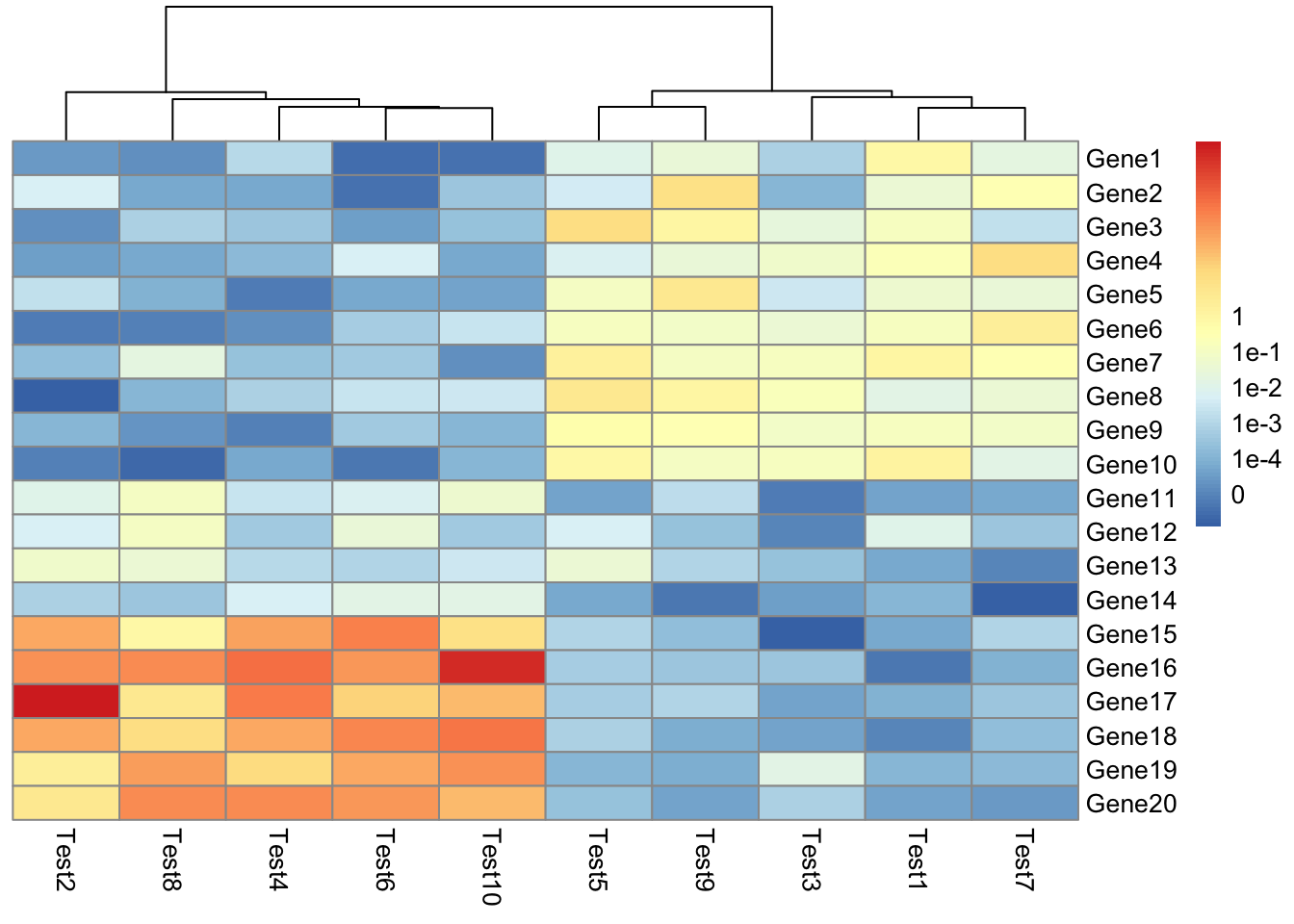
## phetmp> # Fix cell sizes and save to file with correct size
## phetmp> pheatmap(test, cellwidth = 15, cellheight = 12, main = "Example heatmap")
## 
## phetmp> pheatmap(test, cellwidth = 15, cellheight = 12, fontsize = 8, filename = "test.pdf")
## 
## phetmp> # Generate annotations for rows and columns
## phetmp> annotation_col = data.frame(
## phetmp+                     CellType = factor(rep(c("CT1", "CT2"), 5)), 
## phetmp+                     Time = 1:5
## phetmp+                 )
## 
## phetmp> rownames(annotation_col) = paste("Test", 1:10, sep = "")
## 
## phetmp> annotation_row = data.frame(
## phetmp+                     GeneClass = factor(rep(c("Path1", "Path2", "Path3"), c(10, 4, 6)))
## phetmp+                 )
## 
## phetmp> rownames(annotation_row) = paste("Gene", 1:20, sep = "")
## 
## phetmp> # Display row and color annotations
## phetmp> pheatmap(test, annotation_col = annotation_col)
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, annotation_legend = FALSE)
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, annotation_row = annotation_row)
## 
## phetmp> # Change angle of text in the columns
## phetmp> pheatmap(test, annotation_col = annotation_col, annotation_row = annotation_row, angle_col = "45")
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, angle_col = "0")
## 
## phetmp> # Specify colors
## phetmp> ann_colors = list(
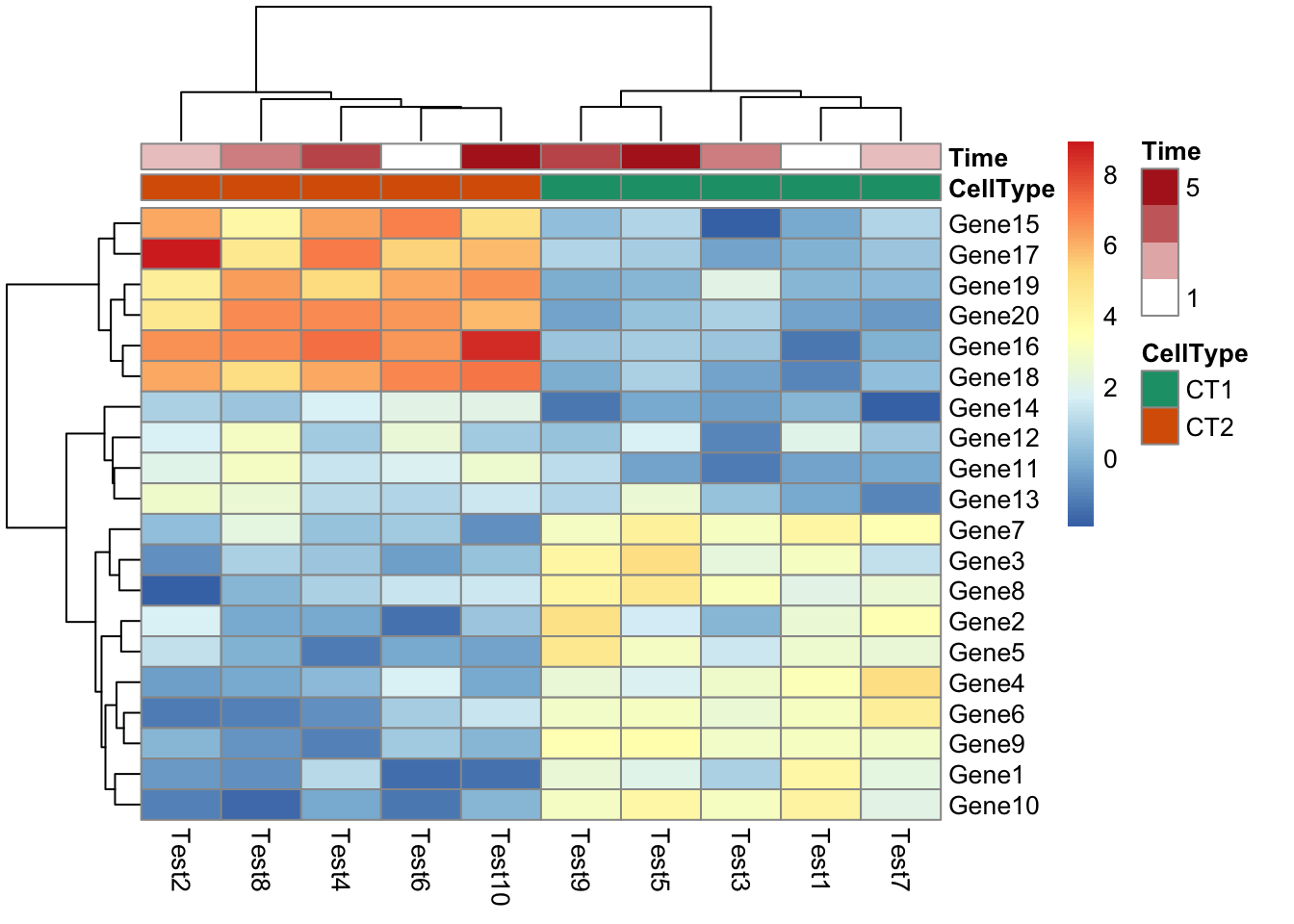
## phetmp+     Time = c("white", "firebrick"),
## phetmp+     CellType = c(CT1 = "#1B9E77", CT2 = "#D95F02"),
## phetmp+     GeneClass = c(Path1 = "#7570B3", Path2 = "#E7298A", Path3 = "#66A61E")
## phetmp+ )
## 
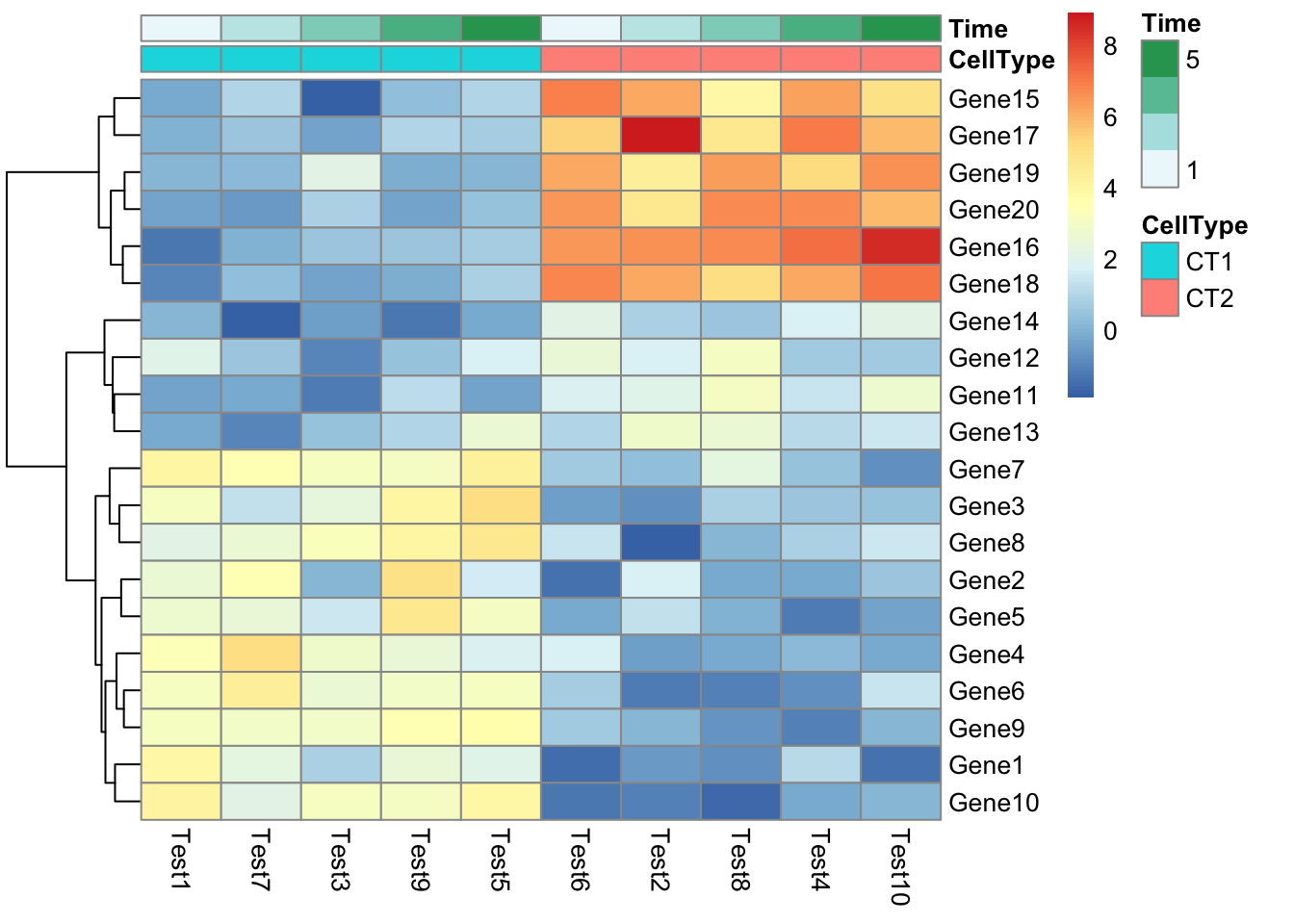
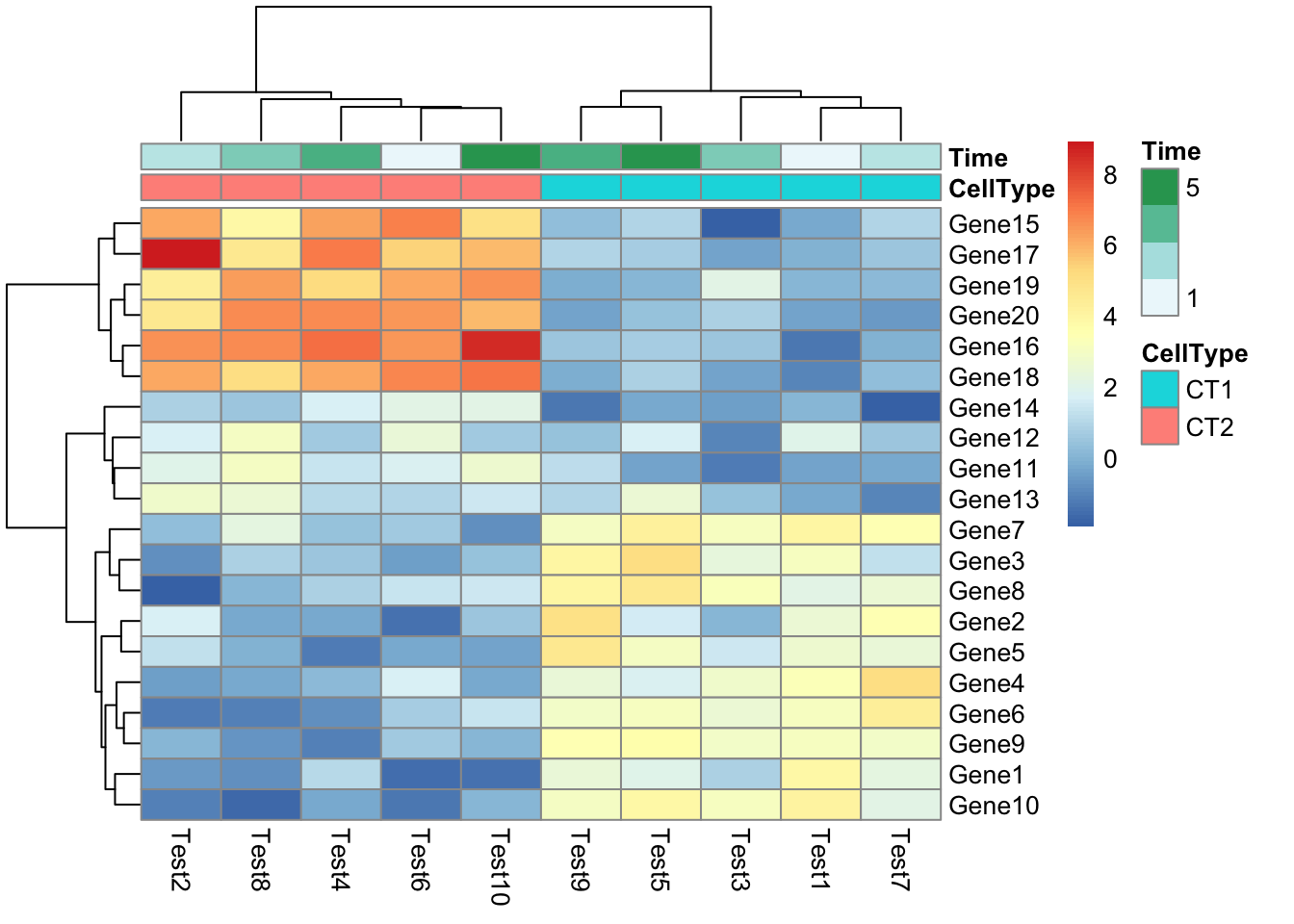
## phetmp> pheatmap(test, annotation_col = annotation_col, annotation_colors = ann_colors, main = "Title")
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, annotation_row = annotation_row, 
## phetmp+          annotation_colors = ann_colors)
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, annotation_colors = ann_colors[2])
## 
## phetmp> # Gaps in heatmaps
## phetmp> pheatmap(test, annotation_col = annotation_col, cluster_rows = FALSE, gaps_row = c(10, 14))
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, cluster_rows = FALSE, gaps_row = c(10, 14), 
## phetmp+          cutree_col = 2)
## 
## phetmp> # Show custom strings as row/col names
## phetmp> labels_row = c("", "", "", "", "", "", "", "", "", "", "", "", "", "", "", 
## phetmp+ "", "", "Il10", "Il15", "Il1b")
## 
## phetmp> pheatmap(test, annotation_col = annotation_col, labels_row = labels_row)
## 
## phetmp> # Specifying clustering from distance matrix
## phetmp> drows = dist(test, method = "minkowski")
## 
## phetmp> dcols = dist(t(test), method = "minkowski")
## 
## phetmp> pheatmap(test, clustering_distance_rows = drows, clustering_distance_cols = dcols)
## 
## phetmp> # Modify ordering of the clusters using clustering callback option
## phetmp> callback = function(hc, mat){
## phetmp+     sv = svd(t(mat))$v[,1]
## phetmp+     dend = reorder(as.dendrogram(hc), wts = sv)
## phetmp+     as.hclust(dend)
## phetmp+ }
## 
## phetmp> pheatmap(test, clustering_callback = callback)
## 
## phetmp> ## Not run: 
## phetmp> ##D # Same using dendsort package
## phetmp> ##D library(dendsort)
## phetmp> ##D 
## phetmp> ##D callback = function(hc, ...){dendsort(hc)}
## phetmp> ##D pheatmap(test, clustering_callback = callback)
## phetmp> ## End(Not run)
## phetmp> 
## phetmp> 
## phetmp> 
## phetmp>

Check “test” data.frame used in pheatmap

test # used in pheatmap
##              Test1       Test2      Test3      Test4      Test5      Test6
## Gene1   3.87067521 -0.52148463  0.8540679  1.1025823  2.0900816 -1.5808262
## Gene2   2.58012361  1.66147955  0.1264007 -0.2446527  1.5992892 -1.4087496
## Gene3   3.07534085 -0.82356787  2.3691700  0.5082200  5.0526051 -0.4820485
## Gene4   3.36896499 -0.44590195  2.8332593  0.1836371  1.8391822  1.6773282
## Gene5   2.72383732  1.23620371  1.5495560 -1.2564252  2.9695515 -0.2697242
## Gene6   3.10835278 -1.20164879  2.6263214 -0.8284632  3.0976685  0.7695611
## Gene7   4.02838534  0.32304593  3.1340938  0.4155175  4.1638313  0.6130010
## Gene8   2.10136976 -1.81411894  3.2213169  0.8538846  4.6478767  1.4257689
## Gene9   3.15940832  0.04800214  2.9355602 -1.1150639  3.6784761  0.6139766
## Gene10  4.05575054 -1.14369241  3.1743554 -0.2282896  3.9308344 -1.3617990
## Gene11 -0.31740553  2.00089619 -1.2117018  1.4034857 -0.3738571  1.8387247
## Gene12  2.07195177  1.68999830 -0.9570393  0.6584128  1.7512976  2.4369045
## Gene13 -0.24987423  2.77303852  0.4263491  1.0861125  2.5693820  0.9247355
## Gene14  0.08241162  0.87755260 -0.4183517  1.6820780 -0.2853531  2.1090133
## Gene15 -0.21900892  6.13183081 -1.9130865  6.2978984  0.9338894  6.9543967
## Gene16 -1.26680048  6.60509557  0.4698898  7.2227571  0.7077581  6.5156679
## Gene17 -0.02048497  8.91535431 -0.3081655  7.0280605  0.7769423  5.4208391
## Gene18 -1.02108141  6.11864402 -0.3859748  6.1848276  0.8442567  6.8527839
## Gene19  0.03721107  4.27951427  2.1543848  5.1282305  0.1269995  6.1841706
## Gene20 -0.36215567  4.63423971  0.8424467  6.6597342  0.3723237  6.4872020
##              Test7       Test8      Test9      Test10
## Gene1   2.26090566 -0.75467547  2.4827519 -1.41316613
## Gene2   3.46210704 -0.22395665  5.0050974  0.55435266
## Gene3   1.31151257  0.81621795  3.9474228  0.39177664
## Gene4   5.07983354 -0.25131602  2.4208155 -0.23721317
## Gene5   2.51494096 -0.02289354  4.6009868 -0.34468093
## Gene6   4.29279135 -1.06142901  2.9251901  1.35637058
## Gene7   3.48056390  2.22389884  2.9728142 -0.78173447
## Gene8   2.60906726  0.12919352  3.9836670  1.47717855
## Gene9   2.90502823 -0.66608292  3.4953998  0.04325105
## Gene10  2.10491334 -1.59185388  3.0287533  0.06622071
## Gene11 -0.18472983  2.97801370  1.1596691  2.68563338
## Gene12  0.53993086  3.06335088  0.4098599  0.58334800
## Gene13 -0.94380619  2.58513813  0.9578149  1.48024628
## Gene14 -1.82395891  0.51087415 -1.3450828  2.18972358
## Gene15  0.91940578  3.90482072  0.2594961  4.95759229
## Gene16  0.02390916  6.65261383  0.4748640  8.57701345
## Gene17  0.56946823  4.62908074  0.9115281  5.79986425
## Gene18  0.33880997  5.11409509 -0.1024726  7.16366744
## Gene19  0.15822780  6.39151732 -0.1625198  6.61726546
## Gene20 -0.50542543  6.67596772 -0.3299609  5.78289674

Error. “No demo found for toic ‘pheatmap’

demo(pheatmap)

col is drawn as found in “test” data frame

colnames(test)
##  [1] "Test1"  "Test2"  "Test3"  "Test4"  "Test5"  "Test6"  "Test7"  "Test8" 
##  [9] "Test9"  "Test10"
pheatmap(test, annotation_col = annotation_col, annotation_colors = ann_colors[2],cluster_cols=FALSE)

sort “test” by order of interest

annotation_col3 <- annotation_col %>% unite(CellType.Time, CellType,Time) %>% arrange(CellType.Time) %>% separate(CellType.Time,c("CellType","Time")) %>% mutate(CellType=factor(CellType),Time=as.numeric(Time))
str(annotation_col3)
## 'data.frame':	10 obs. of  2 variables:
##  $ CellType: Factor w/ 2 levels "CT1","CT2": 1 1 1 1 1 2 2 2 2 2
##  $ Time    : num  1 2 3 4 5 1 2 3 4 5
test3 <- test[,rownames(annotation_col3)]
#quartz()
pheatmap(test3, annotation_col = annotation_col3,cluster_cols=FALSE)

colustering samples

pheatmap(test3, annotation_col = annotation_col3,cluster_cols=TRUE)

custom color (eg. change color of “Time”)

ann_colors
## $Time
## [1] "white"     "firebrick"
## 
## $CellType
##       CT1       CT2 
## "#1B9E77" "#D95F02" 
## 
## $GeneClass
##     Path1     Path2     Path3 
## "#7570B3" "#E7298A" "#66A61E"
pheatmap(test3, annotation_col = annotation_col3, annotation_colors = ann_colors,cluster_cols=TRUE)

demo()

demo(lm.glm, package = "stats", ask = TRUE)
## 
## 
## 	demo(lm.glm)
## 	---- ~~~~~~
## 
## > ### Examples from: "An Introduction to Statistical Modelling"
## > ###			By Annette Dobson
## > ###
## > ### == with some additions ==
## > 
## > #  Copyright (C) 1997-2015 The R Core Team
## > 
## > require(stats); require(graphics)
## 
## > ## Plant Weight Data (Page 9)
## > ctl <- c(4.17,5.58,5.18,6.11,4.50,4.61,5.17,4.53,5.33,5.14)
## 
## > trt <- c(4.81,4.17,4.41,3.59,5.87,3.83,6.03,4.89,4.32,4.69)
## 
## > group <- gl(2,10, labels=c("Ctl","Trt"))
## 
## > weight <- c(ctl,trt)
## 
## > anova  (lm(weight~group))
## Analysis of Variance Table
## 
## Response: weight
##           Df Sum Sq Mean Sq F value Pr(>F)
## group      1 0.6882 0.68820  1.4191  0.249
## Residuals 18 8.7293 0.48496               
## 
## > summary(lm(weight~group -1))
## 
## Call:
## lm(formula = weight ~ group - 1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0710 -0.4938  0.0685  0.2462  1.3690 
## 
## Coefficients:
##          Estimate Std. Error t value Pr(>|t|)    
## groupCtl   5.0320     0.2202   22.85 9.55e-15 ***
## groupTrt   4.6610     0.2202   21.16 3.62e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6964 on 18 degrees of freedom
## Multiple R-squared:  0.9818,	Adjusted R-squared:  0.9798 
## F-statistic: 485.1 on 2 and 18 DF,  p-value: < 2.2e-16
## 
## 
## > ## Birth Weight Data (Page 14)
## > age <- c(40, 38, 40, 35, 36, 37, 41, 40, 37, 38, 40, 38,
## + 	 40, 36, 40, 38, 42, 39, 40, 37, 36, 38, 39, 40)
## 
## > birthw <- c(2968, 2795, 3163, 2925, 2625, 2847, 3292, 3473, 2628, 3176,
## + 	    3421, 2975, 3317, 2729, 2935, 2754, 3210, 2817, 3126, 2539,
## + 	    2412, 2991, 2875, 3231)
## 
## > sex <- gl(2,12, labels=c("M","F"))
## 
## > plot(age, birthw, col=as.numeric(sex), pch=3*as.numeric(sex),
## +      main="Dobson's Birth Weight Data")

## 
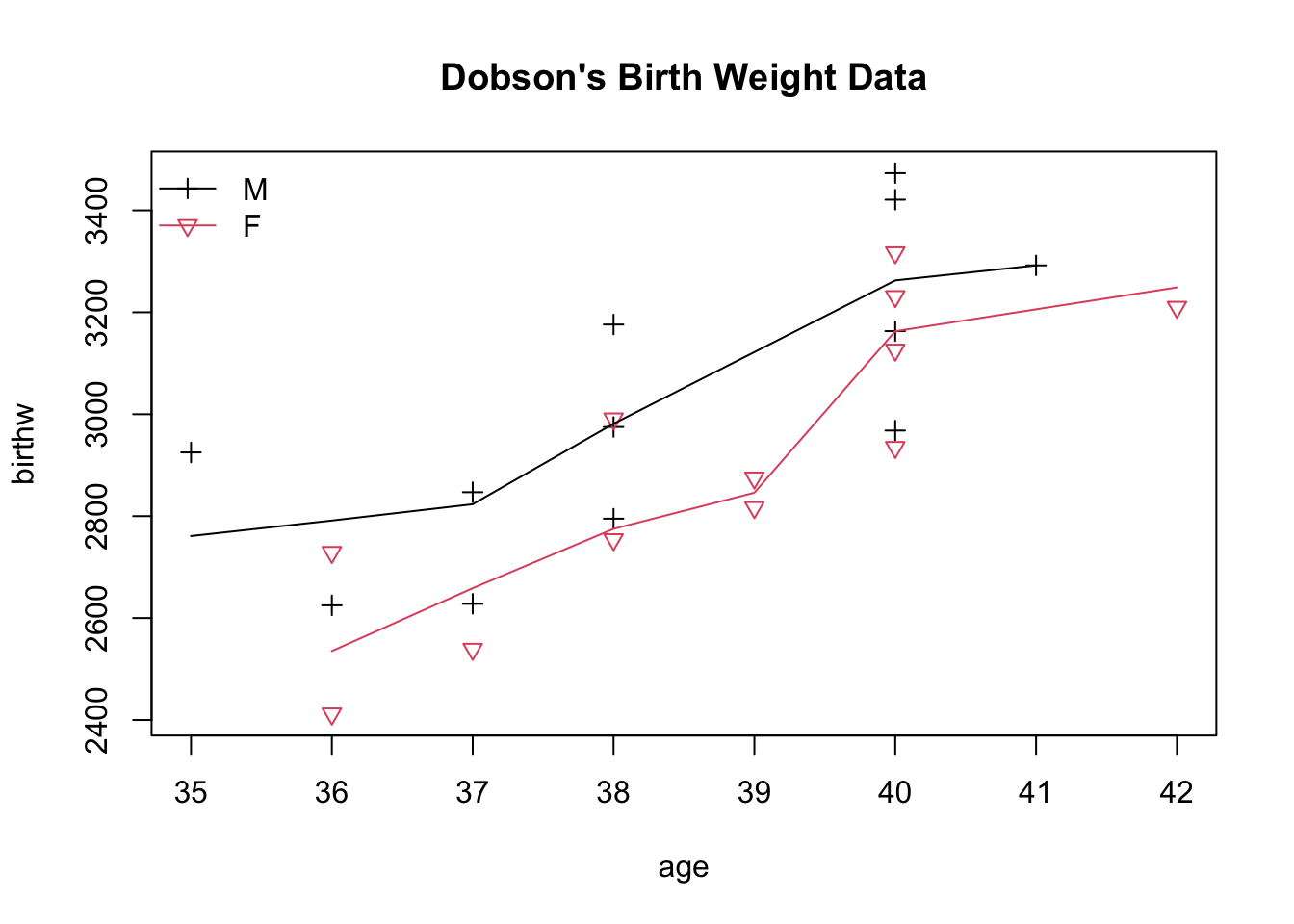
## > lines(lowess(age[sex=='M'], birthw[sex=='M']), col=1)
## 
## > lines(lowess(age[sex=='F'], birthw[sex=='F']), col=2)
## 
## > legend("topleft", levels(sex), col=1:2, pch=3*(1:2), lty=1, bty="n")
## 
## > summary(l1 <- lm(birthw ~ sex + age),    correlation=TRUE)
## 
## Call:
## lm(formula = birthw ~ sex + age)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -257.49 -125.28  -58.44  169.00  303.98 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1610.28     786.08  -2.049   0.0532 .  
## sexF         -163.04      72.81  -2.239   0.0361 *  
## age           120.89      20.46   5.908 7.28e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 177.1 on 21 degrees of freedom
## Multiple R-squared:   0.64,	Adjusted R-squared:  0.6057 
## F-statistic: 18.67 on 2 and 21 DF,  p-value: 2.194e-05
## 
## Correlation of Coefficients:
##      (Intercept) sexF 
## sexF  0.07            
## age  -1.00       -0.12
## 
## 
## > summary(l0 <- lm(birthw ~ sex + age -1), correlation=TRUE)
## 
## Call:
## lm(formula = birthw ~ sex + age - 1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -257.49 -125.28  -58.44  169.00  303.98 
## 
## Coefficients:
##      Estimate Std. Error t value Pr(>|t|)    
## sexM -1610.28     786.08  -2.049   0.0532 .  
## sexF -1773.32     794.59  -2.232   0.0367 *  
## age    120.89      20.46   5.908 7.28e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 177.1 on 21 degrees of freedom
## Multiple R-squared:  0.9969,	Adjusted R-squared:  0.9965 
## F-statistic:  2258 on 3 and 21 DF,  p-value: < 2.2e-16
## 
## Correlation of Coefficients:
##      sexM  sexF 
## sexF  1.00      
## age  -1.00 -1.00
## 
## 
## > anova(l1,l0)
## Analysis of Variance Table
## 
## Model 1: birthw ~ sex + age
## Model 2: birthw ~ sex + age - 1
##   Res.Df    RSS Df   Sum of Sq F Pr(>F)
## 1     21 658771                        
## 2     21 658771  0 -4.8894e-09         
## 
## > summary(li <- lm(birthw ~ sex + sex:age -1), correlation=TRUE)
## 
## Call:
## lm(formula = birthw ~ sex + sex:age - 1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -246.69 -138.11  -39.13  176.57  274.28 
## 
## Coefficients:
##          Estimate Std. Error t value Pr(>|t|)    
## sexM     -1268.67    1114.64  -1.138 0.268492    
## sexF     -2141.67    1163.60  -1.841 0.080574 .  
## sexM:age   111.98      29.05   3.855 0.000986 ***
## sexF:age   130.40      30.00   4.347 0.000313 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 180.6 on 20 degrees of freedom
## Multiple R-squared:  0.9969,	Adjusted R-squared:  0.9963 
## F-statistic:  1629 on 4 and 20 DF,  p-value: < 2.2e-16
## 
## Correlation of Coefficients:
##          sexM  sexF  sexM:age
## sexF      0.00               
## sexM:age -1.00  0.00         
## sexF:age  0.00 -1.00  0.00   
## 
## 
## > anova(li,l0)
## Analysis of Variance Table
## 
## Model 1: birthw ~ sex + sex:age - 1
## Model 2: birthw ~ sex + age - 1
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)
## 1     20 652425                           
## 2     21 658771 -1   -6346.2 0.1945 0.6639
## 
## > summary(zi <- glm(birthw ~ sex + age, family=gaussian()))
## 
## Call:
## glm(formula = birthw ~ sex + age, family = gaussian())
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1610.28     786.08  -2.049   0.0532 .  
## sexF         -163.04      72.81  -2.239   0.0361 *  
## age           120.89      20.46   5.908 7.28e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 31370.04)
## 
##     Null deviance: 1829873  on 23  degrees of freedom
## Residual deviance:  658771  on 21  degrees of freedom
## AIC: 321.39
## 
## Number of Fisher Scoring iterations: 2
## 
## 
## > summary(z0 <- glm(birthw ~ sex + age - 1, family=gaussian()))
## 
## Call:
## glm(formula = birthw ~ sex + age - 1, family = gaussian())
## 
## Coefficients:
##      Estimate Std. Error t value Pr(>|t|)    
## sexM -1610.28     786.08  -2.049   0.0532 .  
## sexF -1773.32     794.59  -2.232   0.0367 *  
## age    120.89      20.46   5.908 7.28e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 31370.04)
## 
##     Null deviance: 213198964  on 24  degrees of freedom
## Residual deviance:    658771  on 21  degrees of freedom
## AIC: 321.39
## 
## Number of Fisher Scoring iterations: 2
## 
## 
## > anova(zi, z0)
## Analysis of Deviance Table
## 
## Model 1: birthw ~ sex + age
## Model 2: birthw ~ sex + age - 1
##   Resid. Df Resid. Dev Df    Deviance F Pr(>F)
## 1        21     658771                        
## 2        21     658771  0 -2.3283e-10         
## 
## > summary(z.o4 <- update(z0, subset = -4))
## 
## Call:
## glm(formula = birthw ~ sex + age - 1, family = gaussian(), subset = -4)
## 
## Coefficients:
##      Estimate Std. Error t value Pr(>|t|)    
## sexM -2318.03     801.57  -2.892  0.00902 ** 
## sexF -2455.44     803.79  -3.055  0.00625 ** 
## age    138.50      20.71   6.688 1.65e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 26925.39)
## 
##     Null deviance: 204643339  on 23  degrees of freedom
## Residual deviance:    538508  on 20  degrees of freedom
## AIC: 304.68
## 
## Number of Fisher Scoring iterations: 2
## 
## 
## > summary(zz <- update(z0, birthw ~ sex+age-1 + sex:age))
## 
## Call:
## glm(formula = birthw ~ sex + age + sex:age - 1, family = gaussian())
## 
## Coefficients:
##          Estimate Std. Error t value Pr(>|t|)    
## sexM     -1268.67    1114.64  -1.138 0.268492    
## sexF     -2141.67    1163.60  -1.841 0.080574 .  
## age        111.98      29.05   3.855 0.000986 ***
## sexF:age    18.42      41.76   0.441 0.663893    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 32621.23)
## 
##     Null deviance: 213198964  on 24  degrees of freedom
## Residual deviance:    652425  on 20  degrees of freedom
## AIC: 323.16
## 
## Number of Fisher Scoring iterations: 2
## 
## 
## > anova(z0,zz)
## Analysis of Deviance Table
## 
## Model 1: birthw ~ sex + age - 1
## Model 2: birthw ~ sex + age + sex:age - 1
##   Resid. Df Resid. Dev Df Deviance      F Pr(>F)
## 1        21     658771                          
## 2        20     652425  1   6346.2 0.1945 0.6639
## 
## > ## Poisson Regression Data (Page 42)
## > x <- c(-1,-1,0,0,0,0,1,1,1)
## 
## > y <- c(2,3,6,7,8,9,10,12,15)
## 
## > summary(glm(y~x, family=poisson(link="identity")))
## 
## Call:
## glm(formula = y ~ x, family = poisson(link = "identity"))
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   7.4516     0.8841   8.428  < 2e-16 ***
## x             4.9353     1.0892   4.531 5.86e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 18.4206  on 8  degrees of freedom
## Residual deviance:  1.8947  on 7  degrees of freedom
## AIC: 40.008
## 
## Number of Fisher Scoring iterations: 3
## 
## 
## > ## Calorie Data (Page 45)
## > calorie <- data.frame(
## +     carb = c(33,40,37,27,30,43,34,48,30,38,
## + 	     50,51,30,36,41,42,46,24,35,37),
## +     age	 = c(33,47,49,35,46,52,62,23,32,42,
## + 	     31,61,63,40,50,64,56,61,48,28),
## +     wgt	 = c(100, 92,135,144,140,101, 95,101, 98,105,
## + 	     108, 85,130,127,109,107,117,100,118,102),
## +     prot = c(14,15,18,12,15,15,14,17,15,14,
## + 	     17,19,19,20,15,16,18,13,18,14))
## 
## > summary(lmcal <- lm(carb~age+wgt+prot, data= calorie))
## 
## Call:
## lm(formula = carb ~ age + wgt + prot, data = calorie)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.3424  -4.8203   0.9897   3.8553   7.9087 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept) 36.96006   13.07128   2.828  0.01213 * 
## age         -0.11368    0.10933  -1.040  0.31389   
## wgt         -0.22802    0.08329  -2.738  0.01460 * 
## prot         1.95771    0.63489   3.084  0.00712 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.956 on 16 degrees of freedom
## Multiple R-squared:  0.4805,	Adjusted R-squared:  0.3831 
## F-statistic: 4.934 on 3 and 16 DF,  p-value: 0.01297
## 
## 
## > ## Extended Plant Data (Page 59)
## > ctl <-	c(4.17,5.58,5.18,6.11,4.50,4.61,5.17,4.53,5.33,5.14)
## 
## > trtA <- c(4.81,4.17,4.41,3.59,5.87,3.83,6.03,4.89,4.32,4.69)
## 
## > trtB <- c(6.31,5.12,5.54,5.50,5.37,5.29,4.92,6.15,5.80,5.26)
## 
## > group <- gl(3, length(ctl), labels=c("Ctl","A","B"))
## 
## > weight <- c(ctl,trtA,trtB)
## 
## > anova(lmwg <- lm(weight~group))
## Analysis of Variance Table
## 
## Response: weight
##           Df  Sum Sq Mean Sq F value  Pr(>F)  
## group      2  3.7663  1.8832  4.8461 0.01591 *
## Residuals 27 10.4921  0.3886                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## > summary(lmwg)
## 
## Call:
## lm(formula = weight ~ group)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0710 -0.4180 -0.0060  0.2627  1.3690 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   5.0320     0.1971  25.527   <2e-16 ***
## groupA       -0.3710     0.2788  -1.331   0.1944    
## groupB        0.4940     0.2788   1.772   0.0877 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6234 on 27 degrees of freedom
## Multiple R-squared:  0.2641,	Adjusted R-squared:  0.2096 
## F-statistic: 4.846 on 2 and 27 DF,  p-value: 0.01591
## 
## 
## > coef(lmwg)
## (Intercept)      groupA      groupB 
##       5.032      -0.371       0.494 
## 
## > coef(summary(lmwg))#- incl.  std.err,  t- and P- values.
##             Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)    5.032  0.1971284 25.526514 1.936575e-20
## groupA        -0.371  0.2787816 -1.330791 1.943879e-01
## groupB         0.494  0.2787816  1.771996 8.768168e-02
## 
## > ## Fictitious Anova Data (Page 64)
## > y <- c(6.8,6.6,5.3,6.1,7.5,7.4,7.2,6.5,7.8,9.1,8.8,9.1)
## 
## > a <- gl(3,4)
## 
## > b <- gl(2,2, length(a))
## 
## > anova(z <- lm(y~a*b))
## Analysis of Variance Table
## 
## Response: y
##           Df  Sum Sq Mean Sq F value   Pr(>F)   
## a          2 12.7400  6.3700 25.8243 0.001127 **
## b          1  0.4033  0.4033  1.6351 0.248225   
## a:b        2  1.2067  0.6033  2.4459 0.167164   
## Residuals  6  1.4800  0.2467                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## > ## Achievement Scores (Page 70)
## > y <- c(6,4,5,3,4,3,6, 8,9,7,9,8,5,7, 6,7,7,7,8,5,7)
## 
## > x <- c(3,1,3,1,2,1,4, 4,5,5,4,3,1,2, 3,2,2,3,4,1,4)
## 
## > m <- gl(3,7)
## 
## > anova(z <- lm(y~x+m))
## Analysis of Variance Table
## 
## Response: y
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## x          1 36.575  36.575  60.355 5.428e-07 ***
## m          2 16.932   8.466  13.970 0.0002579 ***
## Residuals 17 10.302   0.606                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## > ## Beetle Data (Page 78)
## > dose <- c(1.6907, 1.7242, 1.7552, 1.7842, 1.8113, 1.8369, 1.861, 1.8839)
## 
## > x <- c( 6, 13, 18, 28, 52, 53, 61, 60)
## 
## > n <- c(59, 60, 62, 56, 63, 59, 62, 60)
## 
## > dead <- cbind(x, n-x)
## 
## > summary(     glm(dead ~ dose, family=binomial(link=logit)))
## 
## Call:
## glm(formula = dead ~ dose, family = binomial(link = logit))
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -60.717      5.181  -11.72   <2e-16 ***
## dose          34.270      2.912   11.77   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 284.202  on 7  degrees of freedom
## Residual deviance:  11.232  on 6  degrees of freedom
## AIC: 41.43
## 
## Number of Fisher Scoring iterations: 4
## 
## 
## > summary(     glm(dead ~ dose, family=binomial(link=probit)))
## 
## Call:
## glm(formula = dead ~ dose, family = binomial(link = probit))
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -34.935      2.648  -13.19   <2e-16 ***
## dose          19.728      1.487   13.27   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 284.20  on 7  degrees of freedom
## Residual deviance:  10.12  on 6  degrees of freedom
## AIC: 40.318
## 
## Number of Fisher Scoring iterations: 4
## 
## 
## > summary(z <- glm(dead ~ dose, family=binomial(link=cloglog)))
## 
## Call:
## glm(formula = dead ~ dose, family = binomial(link = cloglog))
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -39.572      3.240  -12.21   <2e-16 ***
## dose          22.041      1.799   12.25   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 284.2024  on 7  degrees of freedom
## Residual deviance:   3.4464  on 6  degrees of freedom
## AIC: 33.644
## 
## Number of Fisher Scoring iterations: 4
## 
## 
## > anova(z, update(z, dead ~ dose -1))
## Analysis of Deviance Table
## 
## Model 1: dead ~ dose
## Model 2: dead ~ dose - 1
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1         6      3.446                          
## 2         7    285.222 -1  -281.78 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## > ## Anther Data (Page 84)
## > ## Note that the proportions below are not exactly
## > ## in accord with the sample sizes quoted below.
## > ## In particular, the last value, 5/9, should have been 0.556 instead of 0.555:
## > n <- c(102,  99,   108,	 76,   81,   90)
## 
## > p <- c(0.539,0.525,0.528,0.724,0.617,0.555)
## 
## > x <- round(n*p)
## 
## > ## x <- n*p
## > y <- cbind(x,n-x)
## 
## > f <- rep(c(40,150,350),2)
## 
## > (g <- gl(2,3))
## [1] 1 1 1 2 2 2
## Levels: 1 2
## 
## > summary(glm(y ~ g*f, family=binomial(link="logit")))
## 
## Call:
## glm(formula = y ~ g * f, family = binomial(link = "logit"))
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)  
## (Intercept)  0.1456719  0.1975451   0.737   0.4609  
## g2           0.7963143  0.3125046   2.548   0.0108 *
## f           -0.0001227  0.0008782  -0.140   0.8889  
## g2:f        -0.0020493  0.0013483  -1.520   0.1285  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 10.45197  on 5  degrees of freedom
## Residual deviance:  0.60387  on 2  degrees of freedom
## AIC: 38.172
## 
## Number of Fisher Scoring iterations: 3
## 
## 
## > summary(glm(y ~ g + f, family=binomial(link="logit")))
## 
## Call:
## glm(formula = y ~ g + f, family = binomial(link = "logit"))
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)  
## (Intercept)  0.306643   0.167629   1.829   0.0674 .
## g2           0.405554   0.174560   2.323   0.0202 *
## f           -0.000997   0.000665  -1.499   0.1338  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 10.4520  on 5  degrees of freedom
## Residual deviance:  2.9218  on 3  degrees of freedom
## AIC: 38.49
## 
## Number of Fisher Scoring iterations: 3
## 
## 
## > ## The "final model"
## > summary(glm.p84 <- glm(y~g,  family=binomial(link="logit")))
## 
## Call:
## glm(formula = y ~ g, family = binomial(link = "logit"))
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)  
## (Intercept)   0.1231     0.1140   1.080   0.2801  
## g2            0.3985     0.1741   2.289   0.0221 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 10.452  on 5  degrees of freedom
## Residual deviance:  5.173  on 4  degrees of freedom
## AIC: 38.741
## 
## Number of Fisher Scoring iterations: 3
## 
## 
## > op <- par(mfrow = c(2,2), oma = c(0,0,1,0))
## 
## > plot(glm.p84) # well ?

## 
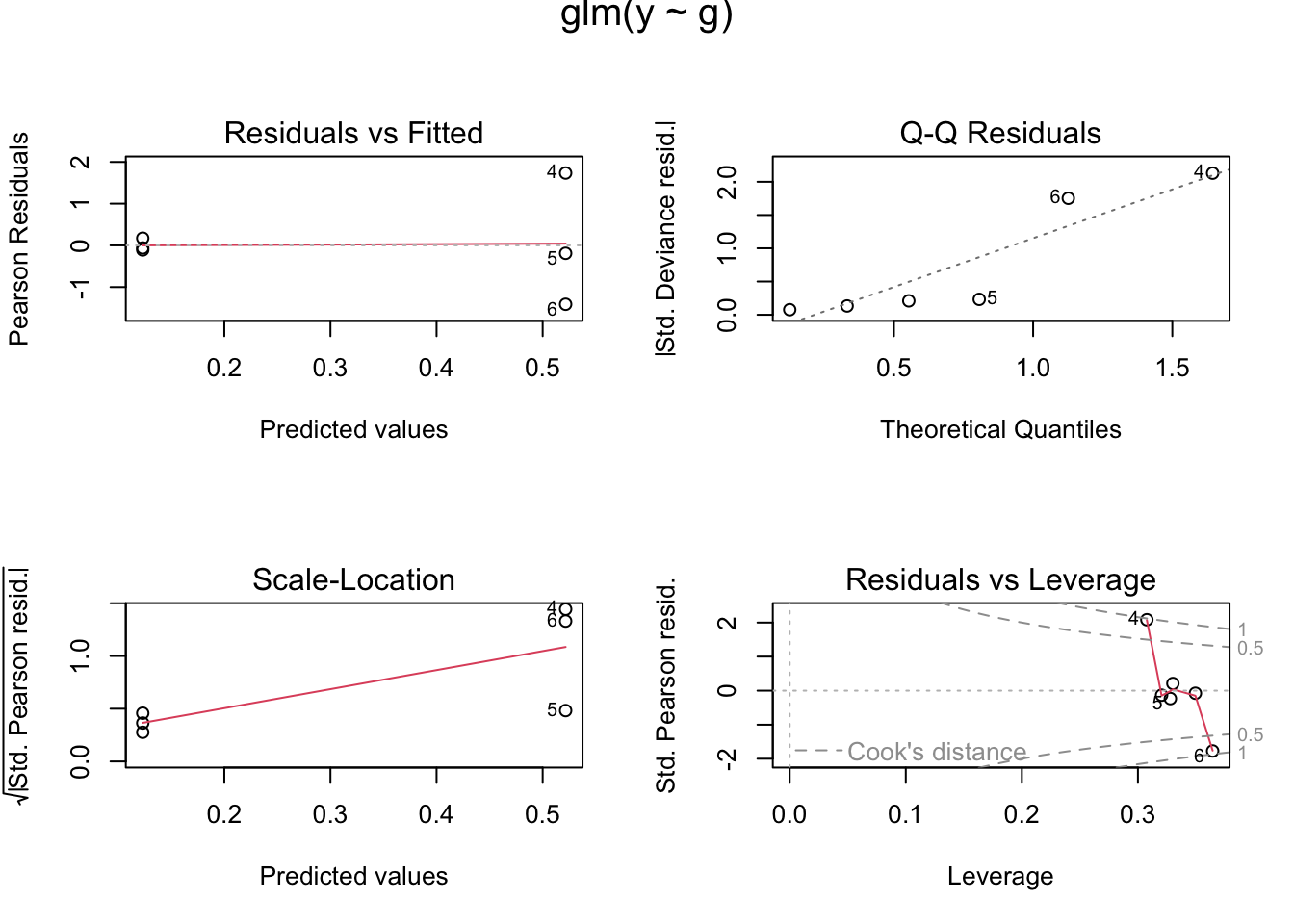
## > par(op)
## 
## > ## Tumour Data (Page 92)
## > counts <- c(22,2,10,16,54,115,19,33,73,11,17,28)
## 
## > type <- gl(4,3,12,labels=c("freckle","superficial","nodular","indeterminate"))
## 
## > site <- gl(3,1,12,labels=c("head/neck","trunk","extremities"))
## 
## > data.frame(counts,type,site)
##    counts          type        site
## 1      22       freckle   head/neck
## 2       2       freckle       trunk
## 3      10       freckle extremities
## 4      16   superficial   head/neck
## 5      54   superficial       trunk
## 6     115   superficial extremities
## 7      19       nodular   head/neck
## 8      33       nodular       trunk
## 9      73       nodular extremities
## 10     11 indeterminate   head/neck
## 11     17 indeterminate       trunk
## 12     28 indeterminate extremities
## 
## > summary(z <- glm(counts ~ type + site, family=poisson()))
## 
## Call:
## glm(formula = counts ~ type + site, family = poisson())
## 
## Coefficients:
##                   Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         1.7544     0.2040   8.600  < 2e-16 ***
## typesuperficial     1.6940     0.1866   9.079  < 2e-16 ***
## typenodular         1.3020     0.1934   6.731 1.68e-11 ***
## typeindeterminate   0.4990     0.2174   2.295  0.02173 *  
## sitetrunk           0.4439     0.1554   2.857  0.00427 ** 
## siteextremities     1.2010     0.1383   8.683  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 295.203  on 11  degrees of freedom
## Residual deviance:  51.795  on  6  degrees of freedom
## AIC: 122.91
## 
## Number of Fisher Scoring iterations: 5
## 
## 
## > ## Randomized Controlled Trial (Page 93)
## > counts <- c(18,17,15, 20,10,20, 25,13,12)
## 
## > outcome   <- gl(3, 1, length(counts))
## 
## > treatment <- gl(3, 3)
## 
## > summary(z <- glm(counts ~ outcome + treatment, family=poisson()))
## 
## Call:
## glm(formula = counts ~ outcome + treatment, family = poisson())
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  3.045e+00  1.709e-01  17.815   <2e-16 ***
## outcome2    -4.543e-01  2.022e-01  -2.247   0.0246 *  
## outcome3    -2.930e-01  1.927e-01  -1.520   0.1285    
## treatment2   1.398e-16  2.000e-01   0.000   1.0000    
## treatment3  -2.416e-16  2.000e-01   0.000   1.0000    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 10.5814  on 8  degrees of freedom
## Residual deviance:  5.1291  on 4  degrees of freedom
## AIC: 56.761
## 
## Number of Fisher Scoring iterations: 4
## 
## 
## > ## Peptic Ulcers and Blood Groups
## > counts <- c(579, 4219, 911, 4578, 246, 3775, 361, 4532, 291, 5261, 396, 6598)
## 
## > group <- gl(2, 1, 12, labels=c("cases","controls"))
## 
## > blood <- gl(2, 2, 12, labels=c("A","O"))
## 
## > city  <- gl(3, 4, 12, labels=c("London","Manchester","Newcastle"))
## 
## > cbind(group, blood, city, counts) # gives internal codes for the factors
##       group blood city counts
##  [1,]     1     1    1    579
##  [2,]     2     1    1   4219
##  [3,]     1     2    1    911
##  [4,]     2     2    1   4578
##  [5,]     1     1    2    246
##  [6,]     2     1    2   3775
##  [7,]     1     2    2    361
##  [8,]     2     2    2   4532
##  [9,]     1     1    3    291
## [10,]     2     1    3   5261
## [11,]     1     2    3    396
## [12,]     2     2    3   6598
## 
## > summary(z1 <- glm(counts ~ group*(city + blood), family=poisson()))
## 
## Call:
## glm(formula = counts ~ group * (city + blood), family = poisson())
## 
## Coefficients:
##                              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                   6.39239    0.03476  183.92  < 2e-16 ***
## groupcontrols                 1.90813    0.03691   51.69  < 2e-16 ***
## cityManchester               -0.89800    0.04815  -18.65  < 2e-16 ***
## cityNewcastle                -0.77420    0.04612  -16.79  < 2e-16 ***
## bloodO                        0.40187    0.03867   10.39  < 2e-16 ***
## groupcontrols:cityManchester  0.84069    0.05052   16.64  < 2e-16 ***
## groupcontrols:cityNewcastle   1.07287    0.04822   22.25  < 2e-16 ***
## groupcontrols:bloodO         -0.23208    0.04043   -5.74 9.46e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 26717.157  on 11  degrees of freedom
## Residual deviance:    29.241  on  4  degrees of freedom
## AIC: 154.32
## 
## Number of Fisher Scoring iterations: 3
## 
## 
## > summary(z2 <- glm(counts ~ group*city + blood, family=poisson()),
## +         correlation = TRUE)
## 
## Call:
## glm(formula = counts ~ group * city + blood, family = poisson())
## 
## Coefficients:
##                              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                   6.51395    0.02663  244.60   <2e-16 ***
## groupcontrols                 1.77563    0.02801   63.38   <2e-16 ***
## cityManchester               -0.89800    0.04815  -18.65   <2e-16 ***
## cityNewcastle                -0.77420    0.04612  -16.79   <2e-16 ***
## bloodO                        0.18988    0.01128   16.84   <2e-16 ***
## groupcontrols:cityManchester  0.84069    0.05052   16.64   <2e-16 ***
## groupcontrols:cityNewcastle   1.07287    0.04822   22.25   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 26717.157  on 11  degrees of freedom
## Residual deviance:    62.558  on  5  degrees of freedom
## AIC: 185.63
## 
## Number of Fisher Scoring iterations: 4
## 
## Correlation of Coefficients:
##                              (Intercept) groupcontrols cityManchester
## groupcontrols                -0.90                                   
## cityManchester               -0.52        0.50                       
## cityNewcastle                -0.55        0.52          0.30         
## bloodO                       -0.23        0.00          0.00         
## groupcontrols:cityManchester  0.50       -0.55         -0.95         
## groupcontrols:cityNewcastle   0.52       -0.58         -0.29         
##                              cityNewcastle bloodO groupcontrols:cityManchester
## groupcontrols                                                                 
## cityManchester                                                                
## cityNewcastle                                                                 
## bloodO                        0.00                                            
## groupcontrols:cityManchester -0.29          0.00                              
## groupcontrols:cityNewcastle  -0.96          0.00   0.32                       
## 
## 
## > anova(z2, z1, test = "Chisq")
## Analysis of Deviance Table
## 
## Model 1: counts ~ group * city + blood
## Model 2: counts ~ group * (city + blood)
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1         5     62.558                          
## 2         4     29.241  1   33.318 7.827e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Session Info

sessionInfo()
## R version 4.4.0 (2024-04-24)
## Platform: aarch64-apple-darwin20
## Running under: macOS Sonoma 14.4
## 
## Matrix products: default
## BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
## LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
## 
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## time zone: America/Los_Angeles
## tzcode source: internal
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## other attached packages:
##  [1] pheatmap_1.0.12 lubridate_1.9.3 forcats_1.0.0   stringr_1.5.1  
##  [5] dplyr_1.1.4     purrr_1.0.2     readr_2.1.5     tidyr_1.3.1    
##  [9] tibble_3.2.1    ggplot2_3.5.1   tidyverse_2.0.0
## 
## loaded via a namespace (and not attached):
##  [1] sass_0.4.9         utf8_1.2.4         generics_0.1.3     blogdown_1.19     
##  [5] stringi_1.8.4      hms_1.1.3          digest_0.6.36      magrittr_2.0.3    
##  [9] evaluate_0.24.0    grid_4.4.0         timechange_0.3.0   RColorBrewer_1.1-3
## [13] bookdown_0.40      fastmap_1.2.0      jsonlite_1.8.8     fansi_1.0.6       
## [17] scales_1.3.0       jquerylib_0.1.4    cli_3.6.3          rlang_1.1.4       
## [21] munsell_0.5.1      withr_3.0.0        cachem_1.1.0       yaml_2.3.9        
## [25] tools_4.4.0        tzdb_0.4.0         colorspace_2.1-0   vctrs_0.6.5       
## [29] R6_2.5.1           lifecycle_1.0.4    pkgconfig_2.0.3    pillar_1.9.0      
## [33] bslib_0.7.0        gtable_0.3.5       glue_1.7.0         xfun_0.46         
## [37] tidyselect_1.2.1   highr_0.11         rstudioapi_0.16.0  knitr_1.48        
## [41] farver_2.1.2       htmltools_0.5.8.1  rmarkdown_2.27     compiler_4.4.0